
Pembahasan soal-soal Ujian Nasional (UN) SMA-IPA bidang studi Fisika dengan materi pembahasan Kapasitor dan Rangkaian Kapasitor.
Soal tentang Kapasitor UN 2009
Kapasitas kapasitor keping sejajar yang diberi muatan dipengaruhi oleh:
A. 2
B. 1 dan
C. 2 dan 4
D. 2 dan 3
E. 1, 3, dan 4
- konstanta dielektrik
- tebal plat
- luas plat
- jarak kedua plat
A. 2
B. 1 dan
C. 2 dan 4
D. 2 dan 3
E. 1, 3, dan 4
Pembahasan
Rumus yang berlaku untuk kapasitas kapasitor keping sejajar adalah
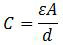
dengan:
C : kapasitas kapasitor
ε : permitivitas dielektrikum (penyekat)
A : luas keping kapasitor
d : jarak antarkeping
Berdasarkan keterangan di atas, pernyataan yang tidak sesuai hanya pernyataan nomor 2.
Jadi, pernyataan yang sesuai dengan kapasitor adalah pernyataan nomor 1, 3, dan 4 (E).
Soal tentang Kapasitor UN 2012
Kapasitor keping sejajar memiliki kapasitas C.

Jika jarak kedua keping diubah menjadi ½-nya dan di antara kedua keping disisipi bahan dielektrik dengan konstanta dielektrik 2, kapasitasnya menjadi ….
A. ½ C
B. ¼ C
C. 2 C
D. 4C
E. 6C

Jika jarak kedua keping diubah menjadi ½-nya dan di antara kedua keping disisipi bahan dielektrik dengan konstanta dielektrik 2, kapasitasnya menjadi ….
A. ½ C
B. ¼ C
C. 2 C
D. 4C
E. 6C

Pembahasan
Kapasitor keping sejajar memiliki kapasitas C.C1 = C
Jarak kedua keping diubah menjadi ½-nya.
d2 = ½ d1
Di antara kedua keping disisipi bahan dielektrik dengan konstanta dielektrik 2 (konstanta dielektrikum semula dianggap 1).
ε1 = 1
ε2 = 2
Pernyataan soal maupun gambar tidak menyebutkan adanya pengubahan pada luas keping. Berarti luas keping konstan.
Rumus yang berlaku untuk kapasitor keping sejajar adalah
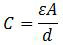
Karena luas keping konstan maka:
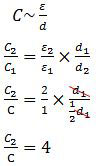
C2 = 4C
Jadi, kapasitas kapasitor tersebut menjadi 4C (D).
Soal Rangkaian Kapasitor UN 2015
Perhatikan gambar rangkaian kapasitor di bawah ini!

Nilai muatan total pada rangkaian kapasitor tersebut adalah ... (1 μF = 10−6 F).
A. 0,5 μC
B. 1 μC
C. 2 μC
D. 4 μC
E. 6 μC

Nilai muatan total pada rangkaian kapasitor tersebut adalah ... (1 μF = 10−6 F).
A. 0,5 μC
B. 1 μC
C. 2 μC
D. 4 μC
E. 6 μC
Pembahasan
Untuk menentukan nilai muatan total, kita cari dulu nilai pengganti kapasitor totalnya. Penghitungan kapasitor pengganti kebalikan dari penghitungan resistor pengganti.
3 kapasitor yang atas adalah identik (nilai kapasitasnya sama) dan tersusun seri. Sehingga nilai kapasitas penggantinya dapat ditentukan dengan rumus

= 1 μF
Sedangkan 2 kapasitor yang bawah tersusun paralel dan identik. Nilai kapasitor penggantinya adalah
Cp = nC
= 2 × 0,5 μF
= 1 μF
Sementara itu, antara rangkaian kapasitor yang atas (Cs) dan rangkaian kapasitor yang bawah (Cp) tersusun paralel. Sehingga kapasitas totalnya adalah
C = Cs + Cp
= 1 μF + 1 μF
= 2μF
Dengan demikian, nilai muatan totalnya adalah
Q = CV
= 2 μF × 3 volt
= 6 μC
Jadi, muatan total rangkaian kapasitor di atas adalah 6 μC (E).
Soal Rangkaian Kapasitor UN 2014
Lima kapasitor C1, C2, C3, C4, dan C5 disusun seperti gambar berikut dan dihubungkan dengan sumber tegangan 6 V.

Muatan listrik pada kapasitor C1 adalah ... (1 μ = 10−6 )
A. 9 μC
B. 18 μC
C. 27 μC
D. 36 μC
E. 45 μC

Muatan listrik pada kapasitor C1 adalah ... (1 μ = 10−6 )
A. 9 μC
B. 18 μC
C. 27 μC
D. 36 μC
E. 45 μC
Pembahasan
Besar muatan listrik pada kapasitor C1 merupakan muatan total (karena belum bercabang). Sehingga kita harus menentukan terlebih dahulu kapasitas totalnya.
Kapasitor C2 dan C3 tersusun seri sehingga kapasitas penggantinya adalah

= 2 μF
Kapasitor seri tersebut tersusun paralel dengan kapasitor C4. Nilai kapasitas penggantinya adalah
Cp = Cs
= 2 μF + 7 μF
= 9 μF
Sedangkan antara C1, Cp, dan C5 tersusun seri. Sehingga kapasitas totalnya adalah

= 4,5 μF
Dengan demikian, muatan listrik yang mengalir pada kapasitor C1 adalah
Q = CV
= 4,5 μF × 6 V
= 27 μC
Jadi, besar muatan listrik pada kapasitor C1 adalah 27 μC (C).
Soal Rangkaian Kapasitor UN 2013
Perhatikan gambar rangkaian kapasitor ini!

Besar energi listrik pada kapasitor gabungan adalah ... (1 μF = 10−6 F).
A. 1,44 × 10−4 joule
B. 2,88 × 10−4 joule
C. 5,76 × 10−4 joule
D. 7,20 × 10−4 joule
E. 8,34 × 10−4 joule

Besar energi listrik pada kapasitor gabungan adalah ... (1 μF = 10−6 F).
A. 1,44 × 10−4 joule
B. 2,88 × 10−4 joule
C. 5,76 × 10−4 joule
D. 7,20 × 10−4 joule
E. 8,34 × 10−4 joule
Pembahasan
Kita tentukan dulu kapasitas totalnya.Kapasitor 7 μF dan 5 μF tersusun paralel, sebut saja Cp1.
Cp1 = 7 μF + 5 μF
= 12 μF
Kapasitor 4 μF dan 2 μF juga tersusun paralel, sebut saja Cp2.
Cp2 = 4 μF + 2 μF
= 6 μF
Sedangkan Cp1, Cp2, dan kapasitor 4 μF yang ada di tengah, tersusun seri. Sehingga kapasitas gabungannya adalah

= 2 μF
Dengan demikian, energi listrik rangkaian di atas adalah
W = ½ CV2
= ½ × 2×10−6 × 242
= 576 × 10−6
= 5,76 × 10−4
Jadi, besar energi listrik pada rangkaian tersebut adalah 5,76 × 10−4 joule (C).
Pembahasan soal Rangkaian Kapasitor yang lain bisa dilihat di:
Pembahasan Fisika UN 2014 No. 29
Pembahasan Fisika UN 2015 No. 34
Pembahasan Fisika UN 2016 No. 36
Pembahasan Fisika UN 2019 No. 32
Simak juga, Pembahasan Fisika UN: Listrik Dinamis.
Dapatkan pembahasan soal dalam file pdf di sini.
Demikian, berbagi pengetahuan bersama Kak Ajaz. Silakan bertanya di kolom komentar apabila ada pembahasan yang kurang jelas. Semoga berkah.

bang itu 4UF nya sama 6uf nya ilang jadi 12uf
ReplyDeleteOh, soal terakhir (Soal Rangkaian Kapasitor UN 2013)
DeleteItu penyebutnya disamakan menjadi 12uF
1/4uF = 3/12uF
1/6uF = 2/12uF
Sehingga:
1/12uF + 1/4uF + 1/6uF
= 1/12uF + 3/12uF + 2/12uF
= (1+3+2)/12uF
thanks
ReplyDeleteSama-sama. Semoga berkah
DeleteKalau energy yang tersimpan dalam rangkaian itu bagamaina carana
ReplyDeletePembahasan yang terakhir (UN 2013) itu menanyakan energi yang tersimpan, cuma redaksi saja yang beda.
DeleteSelain rumus di atas, energi yang tersimpan juga bisa menggunakan rumus berikut (tergantung besaran yang diketahui pada soal):
W = 1/2 QV
W = 1/2 Q^2/V
Jika disoal c1,c2,c3,c4,c5 tuh yang ditanya diganti menjadi c4 gimna caranya?
ReplyDeleteC4 itu kan tersusun paralel dengan Cs (seri C2 dan C3).
DeleteJadi, Q4 = C4/(Cs+C4) x Q
Q = 27 μC (hasil penghitungan pada pembahasan di atas)
Terimakasih, sangat membantu
ReplyDeleteSama-sama. Semoga berkah
Deletebang muatan yang tersimpan dikapasitor 12 u F berapa bang
ReplyDeleteSoal yang mana ya..?
Deleteterimakasih atas pembahasannya..
ReplyDeleteTerima kasih kembali, Fitri. Semoga bermanfaat.
DeleteKalau ditanya c5 bagaimana?
ReplyDeleteMuatan C5 = muatan C1 (untuk soal UN 2014)
DeleteMohon di jawab secepatnya kak :(Sebuah kapasitor terdiri dari dua lempeng alumunium, masing-masing mempunyai luas 14 cm2 dan disekat lapisan mika yang tebalnya 2 mm. Tetapan dielektrik mika 6. Bila diberi beda potensial 12 volt, dan permivitas ruang hampa 8,85 x 10-12 C2/N.m, jumlah muatan yang tersimpan adalah ... .
ReplyDeleteDiketahui:
DeleteA = 14 cm^2 = 14x10^-4 m^2
d = 2 mm = 2x10^-3 m
ε = 6
V = 12
Q = ?
Kapasitas kapasitor keping sejajar dirumuskan:
C = εA/d
= 6 x 14x10^-4 / 2x10^-3
= 4,2 Farad
Jika kapasitor tsb dihubungkan tegangan listrik 12 V maka muatan yang tersimpan adalah:
Q = CV
= 4,2 x 12
= 50,4 C
(Mohon maaf tidak bisa menjawab dengan cepat karena kak ajaz hanya punya waktu malam hari menangani blog ini)
bang klo mau cari energi total yang tersimpan dalam suatu rangkaian gimana? bisa kasih tunjuk contoh nya?
ReplyDeleteSoal yang terakhir itu (UN 2013) menanyakan energi total yang tersimpan, cuma redaksinya saja yang berbeda.
DeletePada soal tersebut ditanyakan "Besar energi listrik pada kapasitor gabungan adalah.."
- Energi kapasitor gabungan = energi total
- Disebut energi yang tersimpan karena fungsi kapasitor adalah menyimpan muatan. Menyimoan muatan berarti menyimpan energi
Kak untuk soal un yang 2015 kalo yang di tanyakan tegangan masing masing setiap kapasitor gimana caranya. Mohon di jawab
ReplyDeleteTegangan pada rangkaian paralel besarnya sama. Karena rangkaian paralel tersebut berhubungan langsung dengan sumber tegangan maka tiap cabang paralel tegangannya 3 volt.
DeleteJad:
- tegangan yang melalui 3 kapasitor 3 μF besarnya 3 volt sehingga tiap kapasitor tegangannya 1 volt
- tegangan yang melalui 2 kapasitor 0,5 μF besarnya 3 volt. Karena keduanya juga tersusun paralel maka tegangan tiap kapasitor juga sama dengan 3 volt
Pak mau nanya kalau soalnya jika kapasitor C1 dan c2 dirangkai seri, kapasitas gabugannya ada di
ReplyDeleteMaksudnya bagaimana ya? Untuk soal no. berapa?
DeleteKalau C1 dan C2 diseri saja maka:
1/Cs = 1/C1 + 1/C2
Kalau mau menghitung muatan pada c1 dan c2 gmana ya caranya ?
ReplyDeleteSoal yang mana ya?
DeleteKalau soal UN 2014, memang muatan C1 yang ditanyakan dan sudah dibahas.